人事コンサルタントの視点

過去コラムにおいて、「統計的有意」についてz検定を用いて解説しましたが、今回のコラムではt検定を用いて解説をしていきたいと思います。解説を読む中で分からない用語があれば、過去コラム「統計的有意とは」も併せて読んでいただければと思います。

t検定とは

t検定とは、2つの集団（標本）の平均値の差に意味があるかを検定する方法です。t検定にはいくつか種類がありますが、本コラムでは独立した2つの集団を扱う「対応のないt検定」におけるスチューデントのt検定について説明します。

例えば、採用における募集方法を変更した際に、昨年の応募者集団と比べて今年の応募者集団に期待した変化が見られているかをOPQで確認する場合や、育成方法を検討するために高業績者とその他社員の違いをOPQで明確化したい場合などで活用できます。

2つの集団（標本）の平均値を単純に比較して異なっていたら良いのではないか、と思われるかもしれません。しかし、標本である以上、その差には必ず偶然のばらつき（サンプリング誤差）が含まれています。このばらつきの影響で、実際には母集団に差がないのに、標本データだけを見ると違いがあるように見えることがあります。そのため、統計的に有意な違いがあるかどうかも含めてデータを評価することで、より的確な施策を打つことができるようになります。

z検定とt検定の違い

z検定もt検定も「平均値の差に意味があるか」を調べる方法ですが、次のような違いがあります。

z検定

1. 母集団のばらつき（分散や標準偏差）が既知の場合に用いる。
2. 標本サイズが大きい場合に適している。
3. 例: OPQ得点は大規模な受検者集団で標準化されており、母集団（一般集団）の平均（5.5）と標準偏差（2）が分かっています。このように、比較対象となる母集団の統計量が既知の場合に、標本の平均値との違いを検定する方法がz検定です。

t検定

1. 母集団のばらつきが未知で、標本データから推定する必要がある場合に用いる。
2. 標本サイズが小さい場合に適している。
3. 例:OPQ得点の母分散は既知ですが、観測された標本のサイズが小さい場合、母分散ではなく標本分散を利用して推定した方が適切であり、t検定を使うのが望ましいです。

このように、母集団の情報がどこまで分かっているか、標本サイズが十分かどうかによって、z検定とt検定の使い分けが必要になります。次に、具体例を用いて詳しく説明していきます。

高業績者とその他社員の比較

企業Aでは開発部門500人（高業績者=100人、その他社員=400人）における業績をあげるべく、育成方法を検討したいと考えています。育成担当者は高業績者とその他社員の違いを「問題解決力」にあるのではないかと考えていますが、データから明確化するために、開発部門500人からランダムに150人（高業績者＝30人、その他社員＝120人）を選択してOPQを実施することにしました。

統計的検定における帰無仮説と対立仮説

高業績者とその他社員とでは「問題解決力」の平均が異なると予想している場合は下記の仮説になります。

帰無仮説：

「問題解決力」における高業績者の母集団平均とその他社員の母集団平均の差は0である

対立仮説：

「問題解決力」における高業績者の母集団平均はその他社員の母集団平均より高い（または低い）

過去コラムでも触れましたが、帰無仮説のもとでは5%以下の確率でしか生じない大きな差の場合、帰無仮説は棄却され、対立仮説が採択されます。これが「統計的に有意に差がある」の考え方になります。

その差は誤差か

OPQ結果より、高業績者30人の「問題解決力」の平均は7.677、標準偏差2.031、その他社員120人の「問題解決力」の平均は5.611、標準偏差2.062でした。

高業績者の母集団平均とその他社員の母集団平均の差が0であれば、高業績者の標本30人の標本平均とその他社員の標本120人の標本平均の差も0となるはずですが、標本から得られた値は0ではなく2.066です。この2.066が母集団から標本がランダムに抽出されたことによる誤差（標準誤差）と判断するのかどうかを計算していきます。

標準誤差の算出

t検定では、2つの標本のばらつきを統合して標準誤差を計算します。これは、2つの標本の平均値の差を検定する際に、各標本のばらつきがどの程度であるかを考慮するためです。なぜなら、データがばらついている標本では平均値の差を見つけにくく、逆にデータがまとまっている標本では敏感に差を検出できるからです。

また、標本サイズが大きい標本は「より正確な情報を提供する」と見なされるため、ばらつきを統合する際には、各標本の分散を標本サイズに応じて加重平均（重み付け）します。これにより、より信頼性の高い標本が差の検出において強調されます。



上記式は、各標本の分散（標準偏差を二乗したもの）を標本サイズに応じて加重平均していることを意味しており、算出された値は統合標準偏差です。
この値に√1高業績標本人数 + 1その他標本人数をかけたものが標準誤差になります。

t値の算出

t値とは、帰無仮説（高業績者の母集団平均とその他社員の母集団平均の差は0である）を基準に、標本データ（高業績者標本平均とその他社員標本平均の差）が、その仮定された差（0）から標準誤差の単位でどれだけ離れているかを算出する指標です。t値が大きいほど、標本データが帰無仮説から大きく離れていることを示し、帰無仮説が棄却される可能性が高まります。


t分布表の自由度148、5%棄却域の値（両側検定の場合2.5%で1.976）よりも大きいと帰無仮説は棄却されます。上記は4.923ですので、帰無仮説は棄却されます。(※自由度=(30-1)+(120-1)=148)

イメージとして捉える

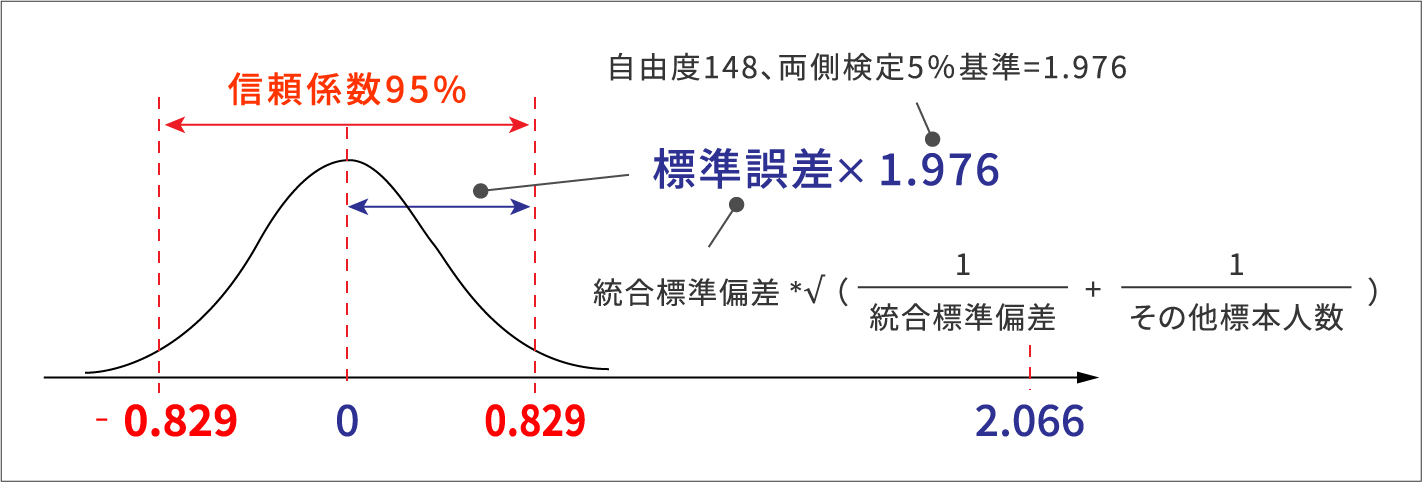
検定統計量の計算としては上記のものになりますが、イメージとして分かりやすくするため、下記に信頼区間と合わせた図を載せます。高評価者の標本30人とその他社員の標本120人が同じ母集団（差が0）から抽出されたのであれば、下記のような信頼区間になりますが、標本平均値差は2.066で区間内に入っていません。よって、帰無仮説は棄却されます。

おわりに

上記例では、高業績者はその他社員と比べて「問題解決力」が統計的に有意に高い（=誤差による差ではない）ことが明らかとなりました。よって、「問題解決力」に関連した育成を行っていこうという判断ができるようになります。実際には、統計的に有意でも、実務的に意味のある差かどうかといった点や、定性的な情報も含めて育成方法については検討していくことになると思いますが、「統計的に有意であるかどうか」は課題に対する解決策の判断に有効な手段の1つだと思います。