データ分析の解釈や分析結果の報告書などに用いられる「統計的有意」という言葉。データ分析が身近になる中で、「統計的有意」がどのような考え方に基づくものか、またどのように算出されるのか疑問を抱く方もいるかと思います。今回はこの「統計的有意」について、関連する用語とともにz検定を用いて解説します。

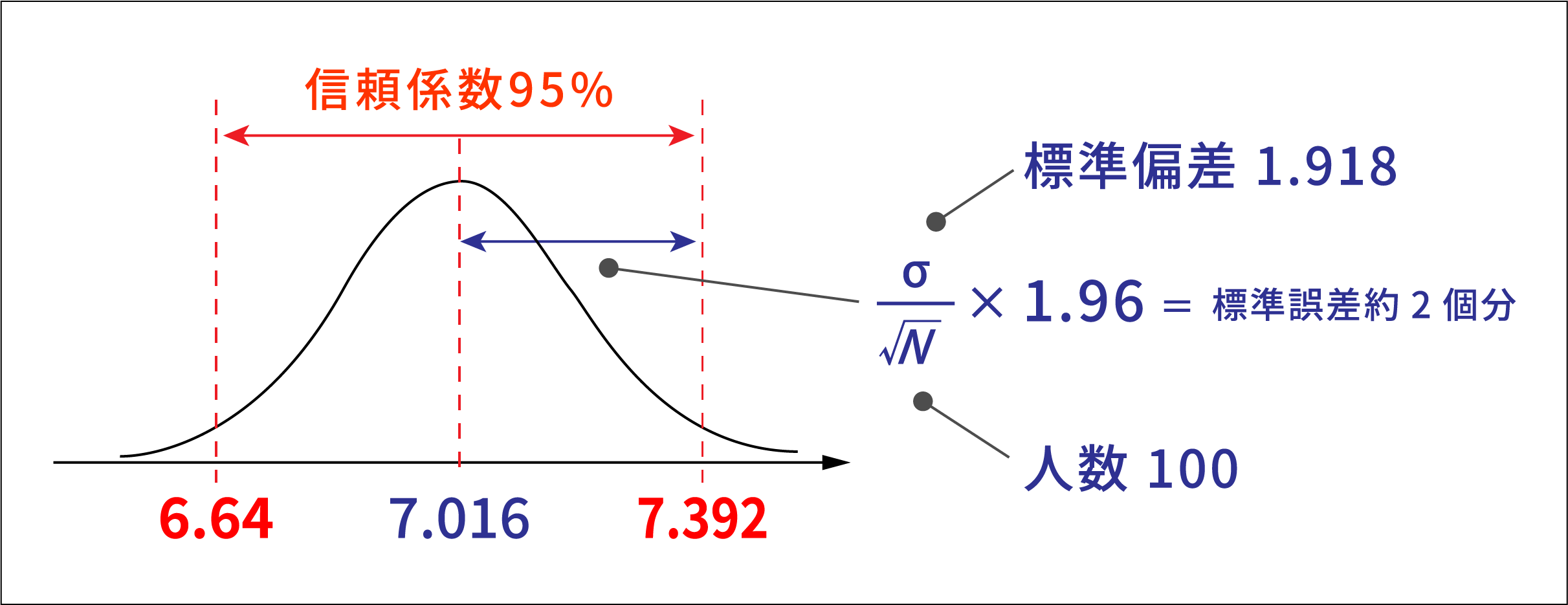
区間推定とは、一つの値ではなく、区間で母集団の平均などを推定することを指します。推定する区間を信頼区間といい、母集団の平均などが信頼区間に含まれる確率を信頼係数といいます。「95%信頼区間」が一般的に用いられることが多いですが、「母集団から100回標本をとりだし、それぞれ母集団の平均の95%信頼区間を求めた場合、95回程度はその区間内に母集団の平均が入る」ことを指します。100人の標本平均が7.016、標準偏差が1.918だった場合、全営業社員の平均(母集団平均)の95%信頼区間は6.64~ 7.392となります。
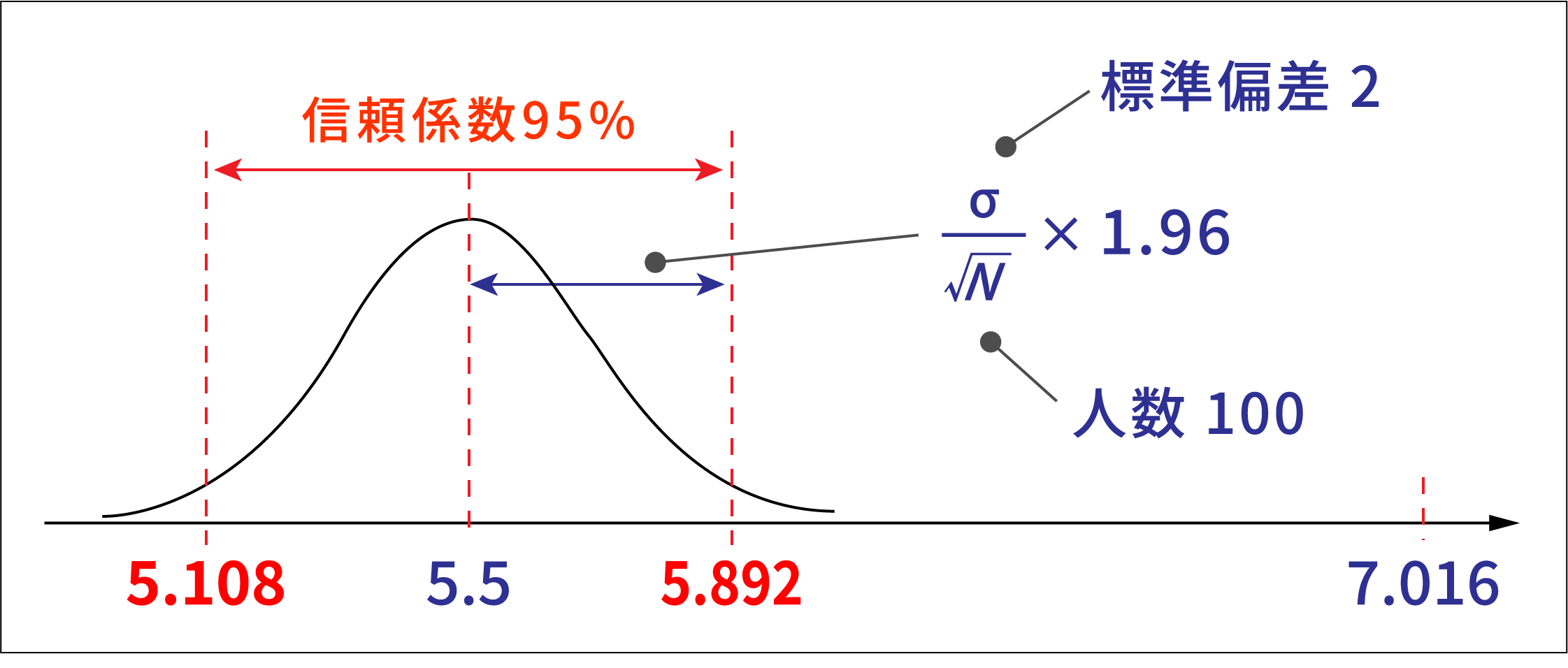
100人の標本平均が帰無仮説のもとでは5%以下の確率でしか生じない大きな値(あるいは小さな値)の場合、帰無仮説は棄却され、対立仮説が採択されます。これが「統計的に有意に差がある」の考え方になります。
全営業社員の標本100人がその母集団(=一般集団)からランダム抽出された集団であれば、下記のような信頼区間となるはずですが、標本平均は7.016ですので、5%よりもずっと低い確率でしか得られない大きな平均値(誤差で生じたとは考えにくい平均値)であると考えられます。よって、全営業社員の「ヴァイタリティ」平均値は5.5である(比較対象集団と同じである)という帰無仮説は棄却され、全営業社員の「ヴァイタリティ」平均値は.比較対象集団と同じでないという対立仮説が採択されることになります。つまり『全営業社員の「ヴァイタリティ」平均値は一般集団よりも統計的に有意に高く、特徴的である』といえるのです。
イメージを捉えるために信頼区間から考えると上記のようになりますが、実際の検定統計量の計算としては下記になります。

このz値が正規分布表の5%棄却域の値(両側検定の場合2.5%で1.96)よりも大きいかどうかによって帰無仮説を棄却するかを判断します。
以上が「統計的有意」の考え方であり、計算の仕方となります。

母集団と標本
はじめに、データを収集するための調査は全数調査と標本調査に分けることができます。知りたいことの対象者全体を母集団といい、母集団全体について調査することを全数調査、その一部を調査することを標本調査といいます。例えば、自社の営業社員(500人)がどういったパーソナリティなのかを知りたいけれど、期間やコスト面から一部の営業社員(100人)にのみパーソナリティ検査OPQを実施する場合は、標本調査となります。全営業社員が母集団、データ収集を行った一部の営業社員が標本といえます。
統計的推定
次に、統計的推定が何かを知っておきましょう。統計的推定とは、母集団のある値(平均値や標準偏差など)を、標本を用いて推定することを指します。標本である100人の営業社員のOPQデータを集計し、「ヴァイタリティ」尺度の平均値が7.016であったとすると、全営業社員の平均(母集団平均)が、標本から7.016と推定されたということになるのです。統計的検定
統計的検定とは母集団に関する予想(「集団Aの平均<集団Bの平均」など)が、正しいといえるかどうかを標本から判断することを指します。例えば、全営業社員(母集団)の「ヴァイタリティ」平均は、比較対象集団の平均より高いという予想を100人の標本から正しいといえるかどうかを判断します。点推定と区間推定
点推定とは、一つの値で母集団の平均などを推定することを指します。上記では全営業社員の「ヴァイタリティ」の平均値は、7.016であると100人の標本から推定していました。点推定は、標本の人数を多くすれば、推定の精度は上がりますが、母集団のものと完全に一致するという可能性は低いです。そこで、その推定がどの程度正しいかを示す指標として標準誤差があります。標準偏差と標準誤差は異なるものです。標準偏差は標本分布のばらつきを示しますが、標準誤差は標本から得られる標本平均(ここでは100人の「ヴァイタリティ」の平均値7.016)のばらつきの大きさを示します。区間推定とは、一つの値ではなく、区間で母集団の平均などを推定することを指します。推定する区間を信頼区間といい、母集団の平均などが信頼区間に含まれる確率を信頼係数といいます。「95%信頼区間」が一般的に用いられることが多いですが、「母集団から100回標本をとりだし、それぞれ母集団の平均の95%信頼区間を求めた場合、95回程度はその区間内に母集団の平均が入る」ことを指します。100人の標本平均が7.016、標準偏差が1.918だった場合、全営業社員の平均(母集団平均)の95%信頼区間は6.64~ 7.392となります。

統計的検定における帰無仮説と対立仮説
帰無仮説は予想が正しいことを主張するために否定したい前提(対立仮説を否定する内容)です。対立仮説は予想している内容、主張したい内容です。例えば、全営業社員の「ヴァイタリティ」平均値が比較対象集団よりも高いと予想している場合は下記の仮説となります。- 帰無仮説:
- 全営業社員の「ヴァイタリティ」平均値は比較対象集団と同じである
- 対立仮説:
- 全営業社員の「ヴァイタリティ」平均値は比較対象集団と同じでない(差がある)
100人の標本平均が帰無仮説のもとでは5%以下の確率でしか生じない大きな値(あるいは小さな値)の場合、帰無仮説は棄却され、対立仮説が採択されます。これが「統計的に有意に差がある」の考え方になります。
z検定
最後に、z検定を用いて理解していきましょう。OPQ得点は大規模な受検者集団で標準化された得点であり、既に母集団(=一般集団)の平均と標準偏差が分かっている分布となります(平均5.5 標準偏差2)。当社ではこの一般集団を比較対象集団として、その平均と標本の平均との差に統計的に意味があるかどうかを検定する方法をz検定としています。全営業社員の標本100人がその母集団(=一般集団)からランダム抽出された集団であれば、下記のような信頼区間となるはずですが、標本平均は7.016ですので、5%よりもずっと低い確率でしか得られない大きな平均値(誤差で生じたとは考えにくい平均値)であると考えられます。よって、全営業社員の「ヴァイタリティ」平均値は5.5である(比較対象集団と同じである)という帰無仮説は棄却され、全営業社員の「ヴァイタリティ」平均値は.比較対象集団と同じでないという対立仮説が採択されることになります。つまり『全営業社員の「ヴァイタリティ」平均値は一般集団よりも統計的に有意に高く、特徴的である』といえるのです。

イメージを捉えるために信頼区間から考えると上記のようになりますが、実際の検定統計量の計算としては下記になります。

このz値が正規分布表の5%棄却域の値(両側検定の場合2.5%で1.96)よりも大きいかどうかによって帰無仮説を棄却するかを判断します。
以上が「統計的有意」の考え方であり、計算の仕方となります。
おわりに
いざ調査、分析、解釈では、「人数が多いと統計的有意になりやすいとは?」「5%有意とは?」等、さまざまな疑問がわいてくると思いますが、疑問解消の参考となれば幸いです。参考図書:岡太彬訓・都築誉史・山口和範 (1995) データ分析のための統計入門 共立出版

このコラムの担当者
水島 奈都代
テスト開発・分析センター 課長





