当社は相関分析と分散分析を一緒に行うことを推奨しています。今回はその理由を解説します。

ケース1
次年度の採用計画を作成するにあたり、採用基準の見直しを検討する企業は多いと思います。この検討に際して、活躍している社員の傾向を見出すために、在籍社員のパーソナリティと成績の関連を調べる分析がよく行われます。この結果を踏まえて現在の採用基準の妥当性を評価し、より適切な新しい採用基準を作成します。
「在籍社員のパーソナリティと成績の関連を調べる」ために最も頻繁に用いられる分析手法が「相関分析」です。相関分析がどのように行われるかについてご説明します。下の図を見てください。
ある企業で活躍している営業職の行動傾向をとらえるための分析を行いました。現職の営業職にパーソナリティ検査OPQを実施してパーソナリティの定量データを取得し、加えて営業成績を基準にハイパフォーマー(HP)、ミドルパフォーマー(MP)、ローパフォーマー(LP)の3群に分け、パフォーマンス評価点を付与しました。これらのデータを使ってパフォーマンス評価点とOPQの各因子得点との相関分析を行った結果が以下のグラフです。
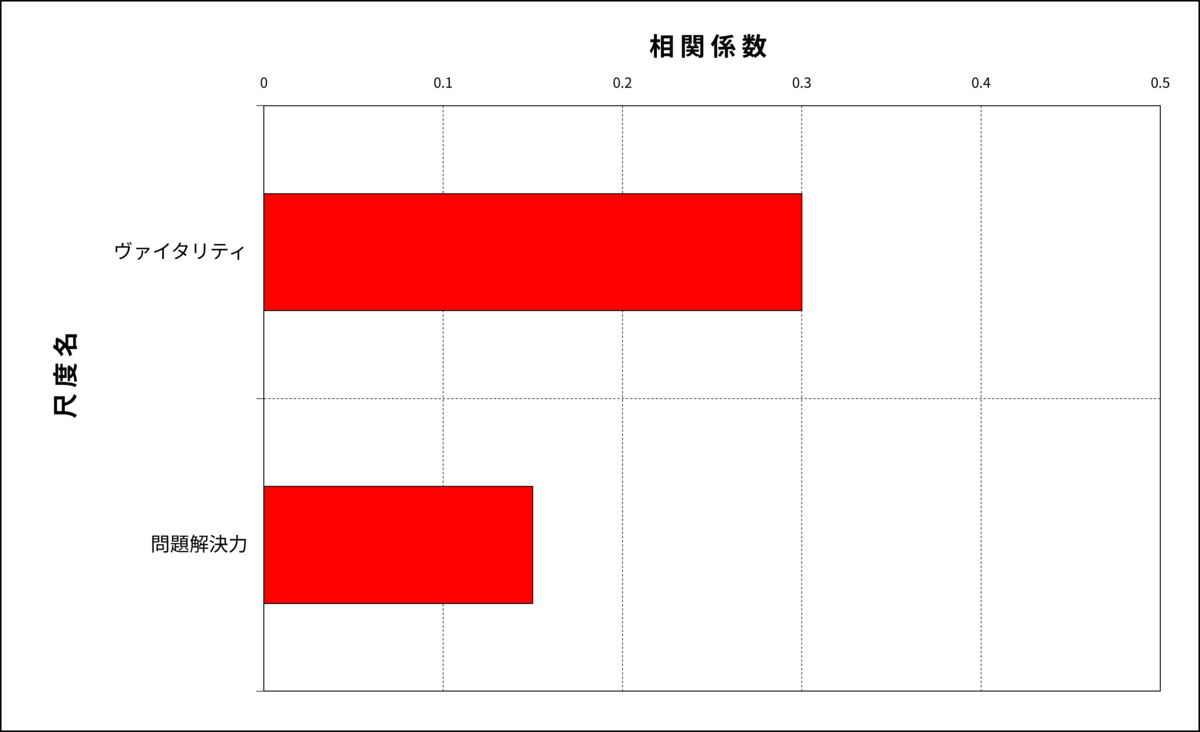
図1:相関分析結果
この図を見ると、パフォーマンス評価点とヴァイタリティ得点との相関係数は0.3であり、パフォーマンス評価点と問題解決力得点との相関係数は0.15となっています。一見するとヴァイタリティのほうが問題解決力よりも営業成績との関係が強くみられますが、同じデータを用いて分散分析を行うとより詳しい情報が得られます。下の図は分散分析の結果です。
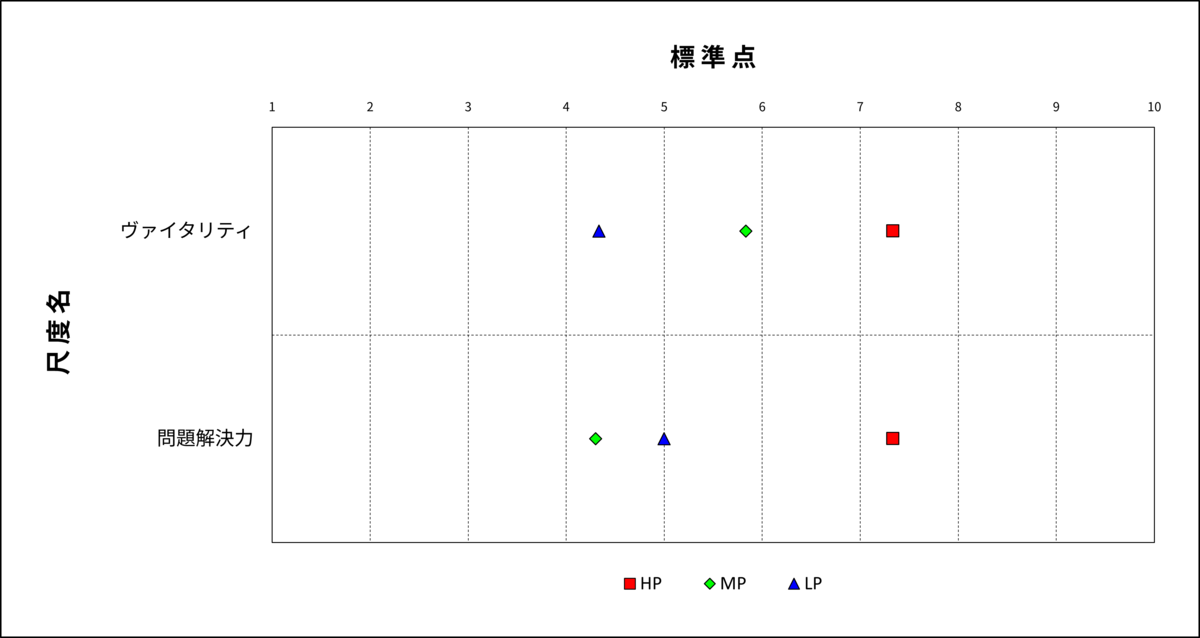
図2:分散分析
この結果を見ると、問題解決力もHPだけの特徴的な尺度として、営業成績と関係がありそうです。
相関分析は数の序列に意味があるので、点数が高ければ営業成績も高くなり、低ければ営業成績も低くなるという一本軸を見つけ出すのに適しています。
しかし、上記の問題解決力のように、ターゲットとなる一群(今回の場合はHP)にだけ特徴的でその他の群間(MPとLP)は差がない場合、あるいは序列通りになっていない場合(LP>MP)は、相関関係にはならないため、相関係数は比較的低くなります。
一方、分散分析は序列に関係なく集団としての特徴を見ているため、集団間の差を見出すことができます。
ケース2
また、こんなケースもあります。下の二つの図を見てください。
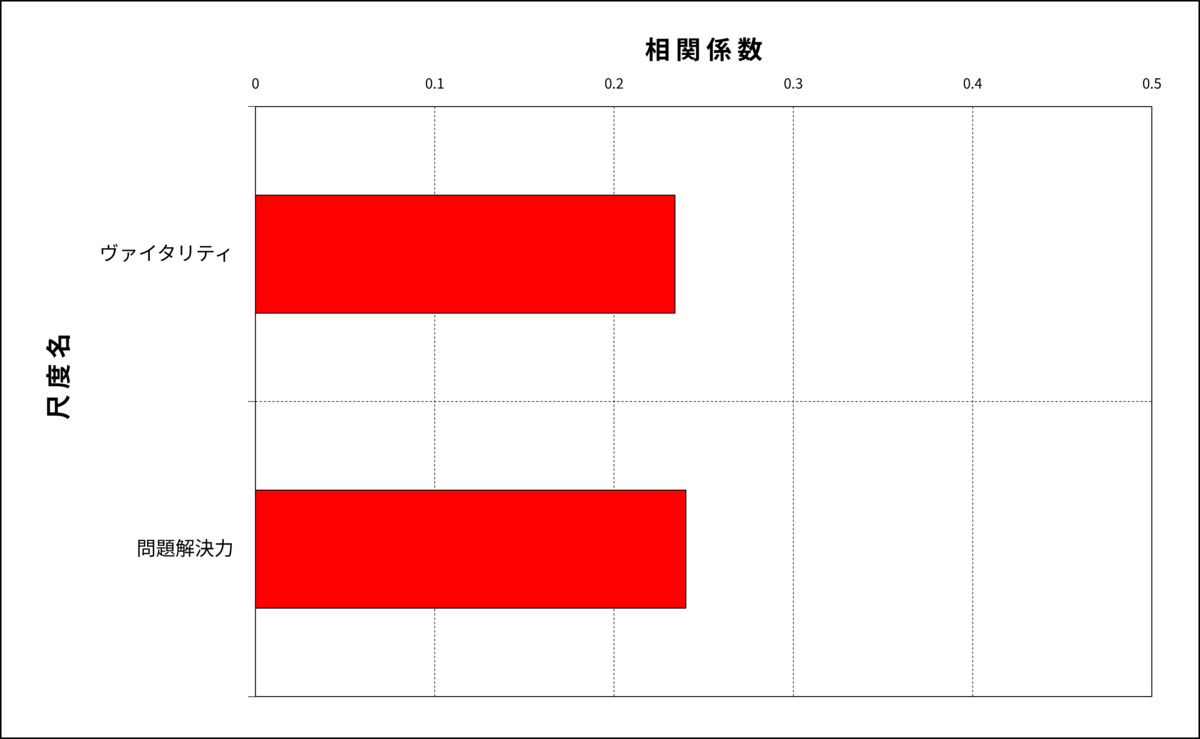
図3:相関分析
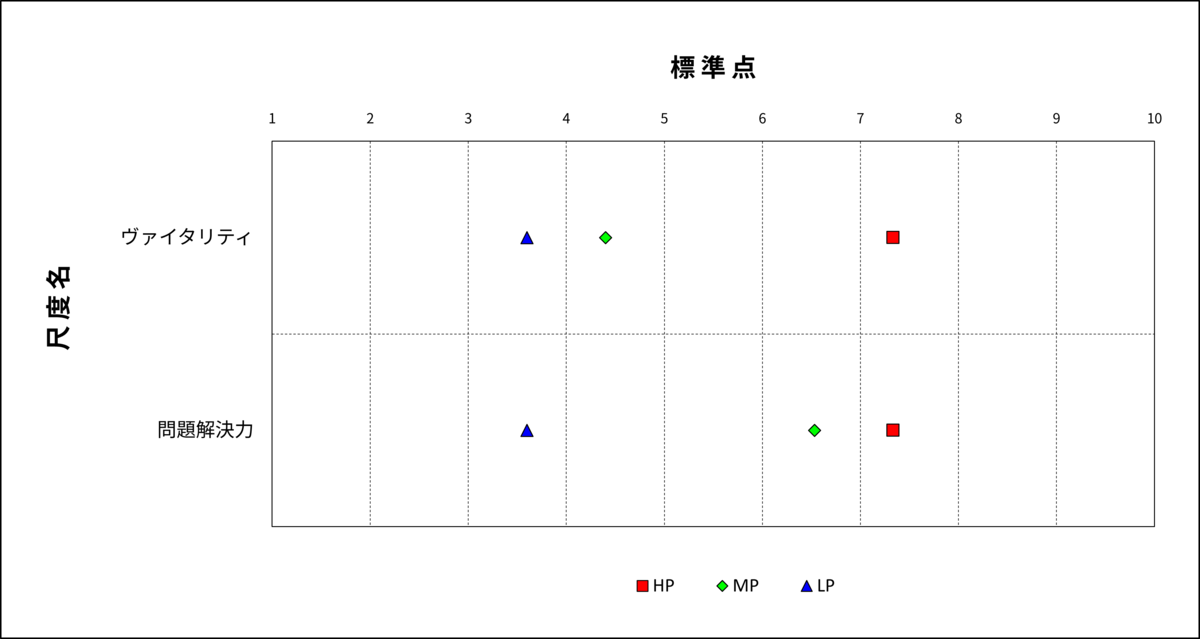
図4:分散分析
どちらも同じくらいの相関係数ですが、分散分析ではヴァイタリティ得点はHPだけが高く、問題解決力得点はLPだけが低くなっています。
ケース3
これらの因子得点を採用選考の初期段階で活用する場合、ヴァイタリティはHPのすくい上げに使えますが、LPの足切りには向かないことがわかります。逆に問題解決力はLPの足切りに向いていますが、HPのすくい上げには向きません。
さらにこんなケースもあります。
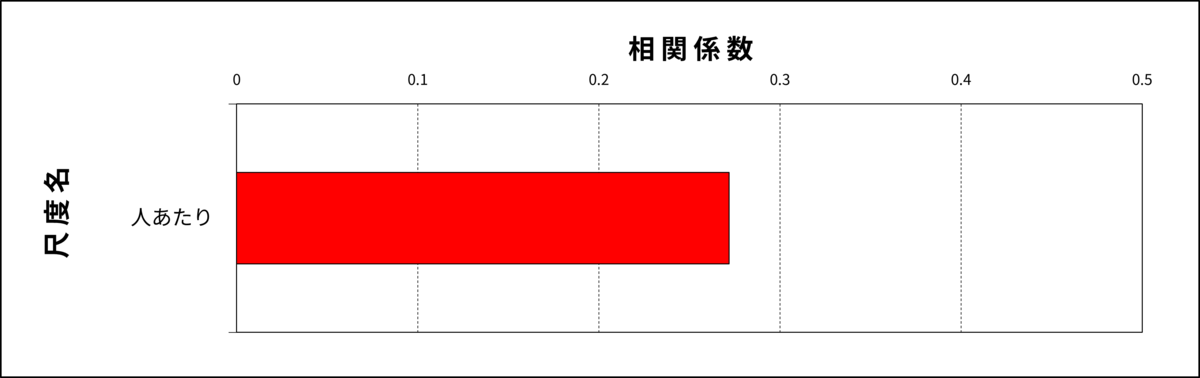
図5:相関分析

図6:分散分析
この場合、HPでも平均値が基準母集団平均(5.5点)よりも低いため、相関分析の結果だけを見て、人あたりの高得点者をすくい上げると現職のHPとは異なる特徴を持つ集団となってしまう可能性があります。
おわりに
このように、相関分析だけではテスト結果を正しく解釈し、運用するための情報として不十分なケースがあるのです。
分散分析、ヒストグラムなどの複数の分析手法やデータ集計方法を組み合わせることで、より適切な解釈を行うことが可能となります。相関分析だけでは活用ができないということではありません。分析を行う目的次第です。当社で請け負う分析の場合、成績とパーソナリティの関係を分析し、その結果をテストによる選抜に利用すること多いため、相関分析だけではなく他の手法も組み合わせることを推奨しています。
※図は全てイメージです。実際のデータから作成したものではありません。

このコラムの担当者
柳島 真理子
テスト開発・分析センター
2010年入社。5年間のHRコンサルタント経験を経て、現在はテスト開発・分析部門にて10年以上にわたりアセスメントの品質管理と新商品開発に従事。コンサルタント時代の採用・育成支援で培った知見を活かし、のべ300社以上のデータ分析支援実績を持つ。営業職の要件定義やストレス要因予測、モチベーションの性差に関する論文を発表。現場感覚を活かしつつ、R&D部門の技術的知見から顧客の組織課題解決に貢献している。


















